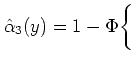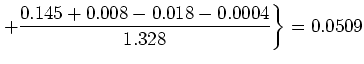

Next: チューブ座標系
Up: ブートストラップ法の幾何学とスケール変換
Previous: 2ステップ=マルチスケール法
3ステップ=マルチスケール法
各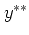 からスケール
からスケール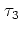 のブートストラップ法によって複製
のブートストラップ法によって複製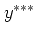 を一
個だけ生成し,スケール
を一
個だけ生成し,スケール
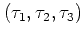 のブートストラップ確率
のブートストラップ確率
を計算する.前節と同様の議論を繰り返すと次式を得る.
ただし
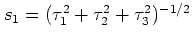 ,
,
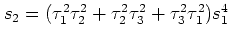 ,
,
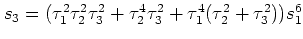 ,
,
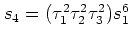 である.
である.
これから係数
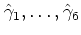 を推定し,
を推定し,
に代入して
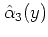 を計算すると,任意の指数型分布族,任意の
を計算すると,任意の指数型分布族,任意の に対して,この3ステップ=マルチスケール法は3次の精度である.
に対して,この3ステップ=マルチスケール法は3次の精度である.
数値例2に適用すると,
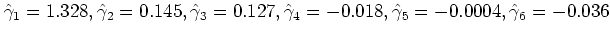 となり,
となり,
が得られる.
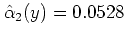 よりもさらに良いことが分かる.
よりもさらに良いことが分かる.
平成16年7月12日
![]() からスケール
からスケール![]() のブートストラップ法によって複製
のブートストラップ法によって複製![]() を一
個だけ生成し,スケール
を一
個だけ生成し,スケール
![]() のブートストラップ確率
のブートストラップ確率
![]() を推定し,
を推定し,
![]() となり,
となり,