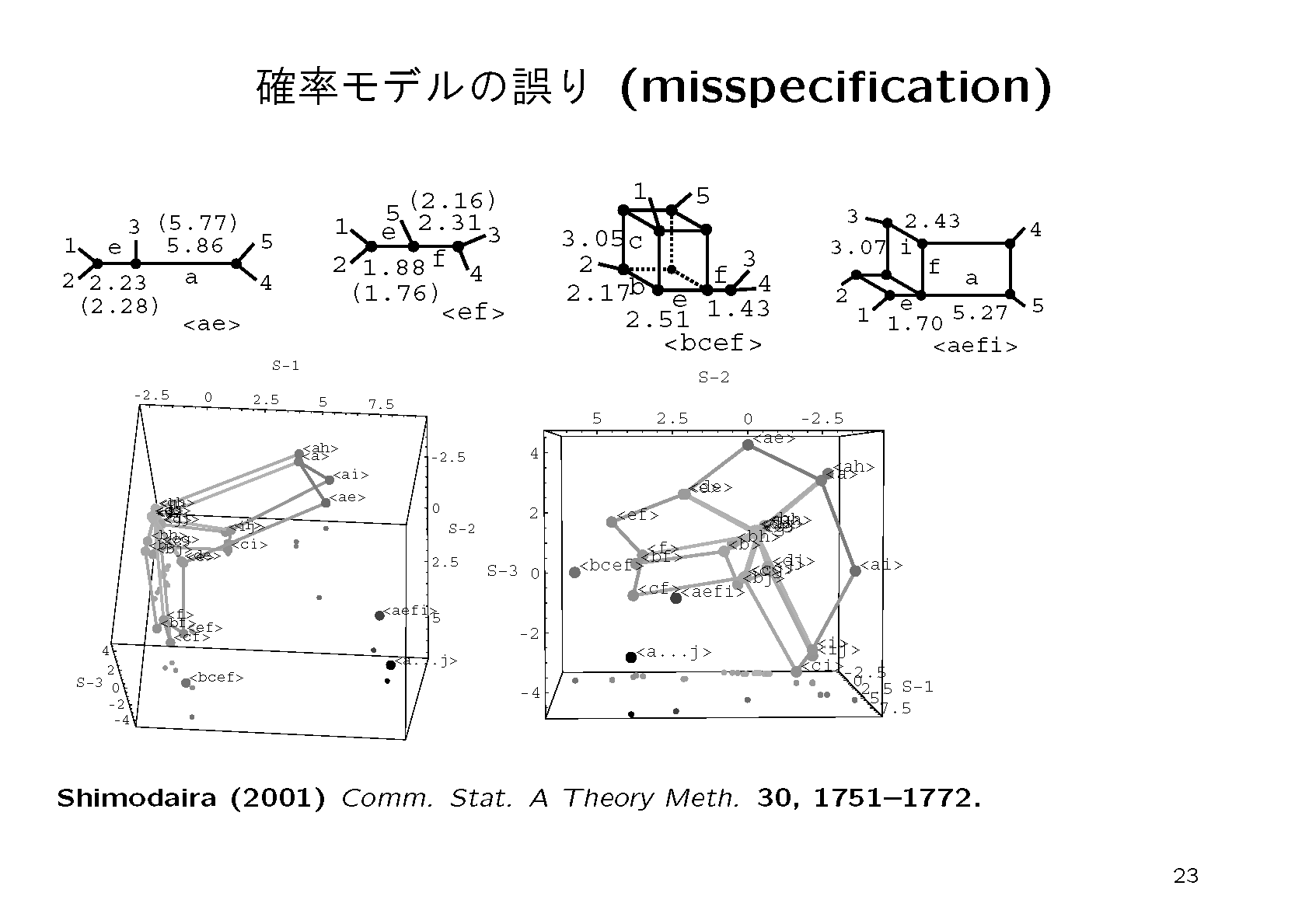
ミトコンドリアゲノムはあまり長くないので系統樹を確定させるには十分な情報を持っていないことがある.とくに非常に古い分岐では推定があいまいになることがある.したがって最尤系統樹以外の系統樹が実は真実である可能性を無視できない.ここでは,プログラムCONSELを用いて系統樹の確率値(p-value)を計算し,真実である可能性が無視できない系統樹をすべて列挙する.
1.さきほど実行したcmd371はwork-conc-user.llsというファイルを出力している.これは系統樹の対数尤度を分解してアミノ酸配列のひとつひとつの列にたいして対数尤度を計算したものであり,これをすべての系統樹に計算したサイズ105 x 3582の行列である.これを用いると,対数尤度のブートストラップ複製というものが計算できる.とくにマルチスケールブートストラップ法といって配列長を10通りかえて計算する方法をここでは用いている. コマンドは
cmd411 [enter]
である.結果はwork-conc-user.rmtというバイナリファイルに格納される.計算のログはwork-conc-rmt.logに書き出される.このコマンドの実行は時間がかかるので,バックグラウンドジョブとして
cmd411 & [enter]
として実行したほうが良いかもしれない.(あやまって何度も同じコマンドを実行しないこと! バックグラウンドジョブのことが良く理解できていないならばやらないこと.) この場合終了したかどうかはログファイルをみて最後に "exit normally"と出ていれば良い.

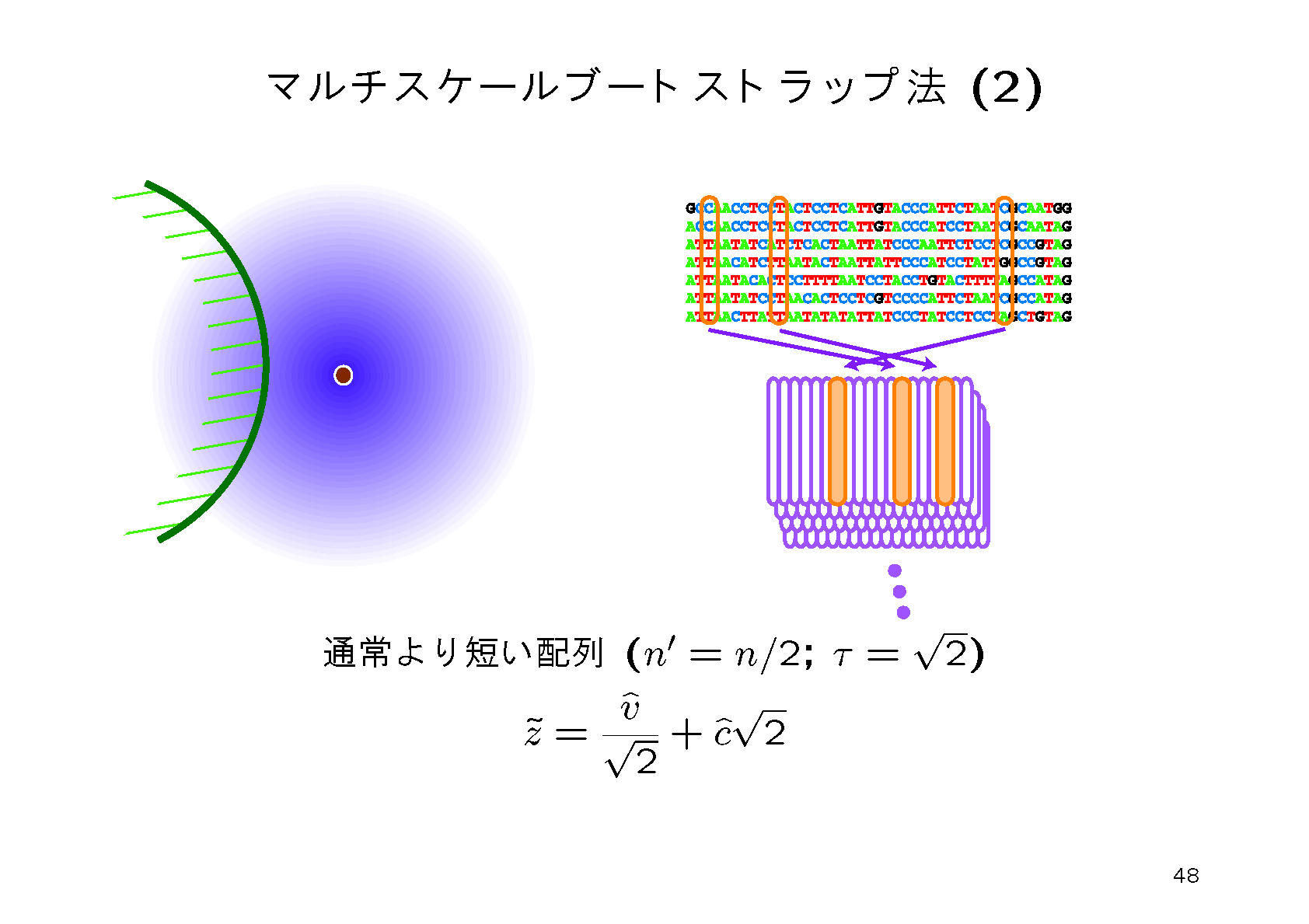




2.系統樹の確率値を計算するコマンドは
cmd431 [enter]
である.結果はwork-conc-tree.logに書かれる.確率値は次のように示されている.
# reading work-conc-tree.pv # 0 1 2 9+ 10 | 3 4 5 6 7 8 # rank item obs au np | bp pp kh sh wkh wsh | # 1 7 -12.7 0.944 0.559 | 0.560 1.000 0.803 1.000 0.803 1.000 | # 2 14 12.7 0.412 0.125 | 0.127 3e-06 0.197 0.879 0.197 0.801 | # 3 12 15.0 0.390 0.077 | 0.071 3e-07 0.154 0.854 0.154 0.732 | # 4 16 20.3 0.303 0.066 | 0.067 2e-09 0.129 0.816 0.129 0.714 | # 5 24 36.7 0.188 0.032 | 0.030 1e-16 0.077 0.534 0.077 0.559 | # 6 17 36.1 0.158 0.038 | 0.038 2e-16 0.081 0.549 0.081 0.566 | # 7 6 36.4 0.142 0.012 | 0.011 2e-16 0.048 0.536 0.048 0.416 | # 8 63 50.9 0.141 0.025 | 0.026 8e-23 0.061 0.314 0.061 0.465 | # 9 1 29.9 0.128 0.014 | 0.013 1e-13 0.036 0.639 0.036 0.345 | # 10 20 40.4 0.118 0.012 | 0.012 3e-18 0.052 0.473 0.052 0.469 | # 11 5 38.8 0.117 0.008 | 0.009 1e-17 0.042 0.490 0.042 0.382 | # 12 62 58.7 0.116 0.011 | 0.010 3e-26 0.032 0.209 0.032 0.366 | # 13 10 37.9 0.085 0.007 | 0.008 3e-17 0.037 0.510 0.037 0.344 | # 14 29 46.5 0.074 0.005 | 0.006 6e-21 0.038 0.376 0.038 0.362 | # 15 9 41.6 0.072 0.004 | 0.003 8e-19 0.026 0.447 0.026 0.283 | # 16 35 61.7 0.057 0.004 | 0.004 2e-27 0.025 0.179 0.025 0.287 |
確率値には色々な定義があるがここでは"au"と書かれた列を見る.この値が0.05以上ならば有意水準5%で棄却できないことをあらわす.ここでは105個中の上位16個が棄却できない.ただしauの大きい順に系統樹が並べられている.work-conc-user.tpl の番号で言うと7, 14, 12, 16, 24 17, 6, 63, 1, 20, 5, 62, 10, 29, 9, 35番めの系統樹である.
3.枝にも確率値を計算することができる.コマンドは
cmd451 [enter]
である.結果はwork-conc-edge.logに書かれる.確率値は次のように示される.
# reading work-conc-edge.pv # 0 1 2 9+ 10 | 3 4 5 6 7 8 # rank item obs au np | bp pp kh sh wkh wsh | # 1 5 -29.9 0.959 0.845 | 0.845 1.000 0.964 0.999 0.919 1.000 | # 2 19 -20.3 0.929 0.805 | 0.803 1.000 0.871 0.995 0.871 0.998 | # 3 1 -12.7 0.856 0.710 | 0.710 1.000 0.803 0.990 0.803 0.996 | # 4 6 12.7 0.251 0.159 | 0.161 3e-06 0.197 0.847 0.197 0.734 | # 5 9 15.0 0.178 0.130 | 0.127 3e-07 0.154 0.823 0.154 0.661 | # 6 20 36.7 0.167 0.032 | 0.030 1e-16 0.077 0.529 0.077 0.525 | # 7 7 20.3 0.165 0.137 | 0.137 2e-09 0.129 0.790 0.129 0.651 | # 8 17 36.1 0.153 0.038 | 0.038 2e-16 0.081 0.546 0.081 0.535 | # 9 16 58.7 0.106 0.011 | 0.010 3e-26 0.032 0.209 0.032 0.345 | # 10 12 50.9 0.098 0.027 | 0.028 8e-23 0.061 0.309 0.061 0.417 | # 11 3 29.9 0.094 0.035 | 0.034 1e-13 0.036 0.626 0.048 0.373 | # 12 14 40.4 0.082 0.022 | 0.022 3e-18 0.052 0.461 0.052 0.421 | # 13 23 46.5 0.071 0.035 | 0.038 6e-21 0.038 0.372 0.061 0.420 |
のようにauが0.05以上になるのは13個の枝であり,番号5, 19, 1, ..., 23である.ただし,この番号がどの枝を意味するかの対応表はwork-conc-ass.logに書かれている.ファイルの中ごろでまず葉の番号を定義してから枝のリストが続く.
# leaves: 25
25
1 NC_001325
2 NC_001602
3 NC_004023
4 NC_004029
5 NC_003428
6 NC_002008
7 NC_001700
8 NC_001640
9 NC_001808
10 NC_000845
11 NC_001567
12 NC_000889
13 NC_001601
14 NC_002503
15 NC_001913
16 NC_001643
17 NC_001644
18 NC_001807
19 NC_001645
20 NC_002083
21 NC_004025
22 NC_002658
23 NC_001569
24 NC_001610
25 NC_000891
# base edges: 25
25 25
1 2
1234567890123456789012345
1 ++++++++++++++++++++++--- ; (0.1429)
2 ++++++++++++++--------+-- ; (0.1429)
3 +++++++++++++++---------- ; (0.1429)
4 ++++++++++++++-++++++++-- ; (0.1429)
5 ++++++++++++++-++++++---- ; (0.1429)
6 +++++++++++++++++++++-+-- ; (0.1429)
7 --------------+------+--- ; (0.1429)
8 --------------+++++++---- ; (0.1429)
9 ---------------------++-- ; (0.1429)
10 ---------------+++++++--- ; (0.1429)
11 ++++++++++++++-------+--- ; (0.1429)
12 +++++++++++++++------++-- ; (0.1429)
13 --------------+++++++++-- ; (0.1429)
14 --------------+-------+-- ; (0.1429)
15 ---------------++++++-+-- ; (0.1429)
16 +++++++++++++++-------+-- ; (0.0857)
17 --------------++++++++--- ; (0.0857)
18 ++++++++++++++-+++++++--- ; (0.0857)
19 +++++++++++++++++++++---- ; (0.0857)
20 +++++++++++++++------+--- ; (0.0857)
21 ++++++++++++++-------++-- ; (0.0857)
22 ---------------++++++++-- ; (0.0857)
23 --------------+------++-- ; (0.0857)
24 --------------+++++++-+-- ; (0.0857)
25 ++++++++++++++-++++++-+-- ; (0.0857)
のように,+と-マークの組み合わせで枝が表現されている.従ってau=0.959でrank=1の枝はitem=5だから
5 ++++++++++++++-++++++---- ;
と表現され,これは(NC_001325,...,NC_002503,NC_001643,...,NC_004025)の生物群についた枝である.これ以降に書かれている枝のリスト
# common edges: 44
44 25
1 2
1234567890123456789012345
26 +++++++++++++++++++++++-- ; (1.0000)
27 ++++++++++++++----------- ; (1.0000)
28 +++++++++---------------- ; (1.0000)
29 +++++++------------------ ; (1.0000)
30 ++++++------------------- ; (1.0000)
31 +++++-------------------- ; (1.0000)
32 ++++--------------------- ; (1.0000)
33 ++----------------------- ; (1.0000)
34 +------------------------ ; (1.0000)
35 -+----------------------- ; (1.0000)
36 --++--------------------- ; (1.0000)
37 --+---------------------- ; (1.0000)
38 ---+--------------------- ; (1.0000)
39 ----+-------------------- ; (1.0000)
40 -----+------------------- ; (1.0000)
41 ------+------------------ ; (1.0000)
42 -------++---------------- ; (1.0000)
43 -------+----------------- ; (1.0000)
44 --------+---------------- ; (1.0000)
45 ---------+++++----------- ; (1.0000)
46 ---------+--------------- ; (1.0000)
47 ----------++++----------- ; (1.0000)
48 ----------+-------------- ; (1.0000)
49 -----------+++----------- ; (1.0000)
50 -----------+------------- ; (1.0000)
51 ------------++----------- ; (1.0000)
52 ------------+------------ ; (1.0000)
53 -------------+----------- ; (1.0000)
54 --------------+---------- ; (1.0000)
55 ---------------++++++---- ; (1.0000)
56 ---------------+++++----- ; (1.0000)
57 ---------------++++------ ; (1.0000)
58 ---------------+++------- ; (1.0000)
59 ---------------++-------- ; (1.0000)
60 ---------------+--------- ; (1.0000)
61 ----------------+-------- ; (1.0000)
62 -----------------+------- ; (1.0000)
63 ------------------+------ ; (1.0000)
64 -------------------+----- ; (1.0000)
65 --------------------+---- ; (1.0000)
66 ---------------------+--- ; (1.0000)
67 ----------------------+-- ; (1.0000)
68 -----------------------+- ; (1.0000)
69 ------------------------+ ; (1.0000)
は105通りの候補系統樹すべてに含まれていたので確率値=1.00である.
4. cmd431の出力はなんとも読みにくい.そこでwork-conc-clade.txtに従って生物群にラベルを付けて結果を整理する.まずwork-conc-user.tplもしくはwork-conc-ass.logから系統樹リストの一覧の部分だけを切り取ってwork-conc-tree-list1.txtを作る.そして
repnamegb -sv -p 4 -l work-conc-clade.txt work-conc-tree-list1.txt > work-conc-tree-list2.txt
と入力してwork-conc-tree-list2.txtを書き出す.そして
sortlines -c 3 -f work-conc-tree.log work-conc-tree-list2.txt > work-conc-tree-sort.txt
と入力するとwork-conc-tree-sort.txtが書き出される.これは系統樹のラベルをwork-conc-clade.txtで定義したものに置き換えた上でauの大きい順に系統樹を並び替えたものである.この上位16個
(((((A,B),C),D),E),F); 7 <- 7 (0.0095) (((((A,B),C),E),D),F); 14 <- 14 (0.0095) ((((A,B),C),(D,E)),F); 12 <- 12 (0.0095) ((((A,B),(C,D)),E),F); 16 <- 16 (0.0095) ((((A,(C,D)),B),E),F); 24 <- 24 (0.0095) (((A,(B,(C,D))),E),F); 17 <- 17 (0.0095) ((((A,C),B),(D,E)),F); 6 <- 6 (0.0095) (((A,(C,(D,E))),B),F); 63 <- 63 (0.0095) (((((A,C),B),D),E),F); 1 <- 1 (0.0095) ((((A,B),(C,E)),D),F); 20 <- 20 (0.0095) (((((A,C),B),E),D),F); 5 <- 5 (0.0095) ((((A,(C,E)),B),D),F); 62 <- 62 (0.0095) (((A,(B,C)),(D,E)),F); 10 <- 10 (0.0095) (((A,B),(C,(D,E))),F); 29 <- 29 (0.0095) ((((A,(B,C)),E),D),F); 9 <- 9 (0.0095) ((A,(B,(C,(D,E)))),F); 35 <- 35 (0.0095)
が系統樹の信頼集合である.
4.cmd451の出力も読みにくい.そこでwork-conc-clade.txtに従って生物群にラベルを付けて結果を整理する.まずwork-conc-ass.logから枝リストの一覧の部分だけを切り取ってwork-conc-edge-list1.txtを作る.そして今度は手作業でラベル付けを行いwork-conc-edge-list2.txtを作成する.#のついた行はコメントなので無視される.そして,
sortlines -c 3 -f work-conc-edge.log work-conc-edge-list2.txt > work-conc-edge-sort.txt
で結果をソートしてwork-conc-edge-sort.txtを作成する.この上位13個の枝をみると
5 ++++++++++++++-++++++---- ; (A,B) 19 +++++++++++++++++++++---- ; (A,B,C) 1 ++++++++++++++++++++++--- ; (A,B,C,D) 6 +++++++++++++++++++++-+-- ; (A,B,C,E) 9 ---------------------++-- ; (D,E) 20 +++++++++++++++------+--- ; (A,C,D) 7 --------------+------+--- ; (C,D) 17 --------------++++++++--- ; (B,C,D) 16 +++++++++++++++-------+-- ; (A,C,E) 12 +++++++++++++++------++-- ; (A,C,D,E) 3 +++++++++++++++---------- ; (A,C) 14 --------------+-------+-- ; (C,E) 23 --------------+------++-- ; (C,D,E)となっていてこれらが枝の信頼集合である.
5.TreeViewという系統樹をグラフィックで表示するソフトを使ってwork-conc-user.phyの系統樹のいくつかを表示してみよう(ただしeduにはtreeviewはインストールされていないのでこれはやらなくてもよい).ここでwork-conc-user.phyはwork-conc-user.treをauの大きい順に並べ替えたものである.
AUを一番大きくするのはitem=7である.この系統樹はwork-conc-sort-root-1.pdf(もしくは根無しで書くとwork-conc-sort-unroot-1.pdf)である.この系統樹が真実であるとすると,これまでの生物学の知識に反する結果であるので,新たな発見をしたことになる.つまり,これまではウサギとネズミは近縁で一つのグループを作ると考えられていたからである.ところがAUの順位で14番目(根有り,根無し)と16番目(根有り,根無し)の系統樹をみると,ここでは古典的な結果が示唆されていて,これらの系統樹もAUが0.05以上になっているので棄却されない.従って,新たな発見をしたとは必ずしもいえないわけだ.
自分で分析した結果に対しても同様の考察をしてみよ.
6.このような系統樹推定のあいまいさは,データのバラツキが本質的な問題であり,データに含まれる情報が有限である以上避けられない問題である.系統樹推定のあいまいさを導くもう一つの問題は,仮定した「進化の確率モデル」があくまでも近似であり,その近似が必ずしも良くないということである.系統樹はグラフ理論のtreeであるが,その制約をとって一般のgraph(つまりネットワーク)としてモデルを構築することも可能である.(この話題はあくまでも参考なので,レポートでは議論しなくて良い).