

Next: 2ステップ=マルチスケール法
Up: ブートストラップ法の幾何学とスケール変換
Previous: マルチスケール・ブートストラップ法
数値例2. 各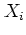 が期待値
が期待値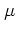 の指数分布に従うとき,
の指数分布に従うとき,
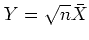 はガンマ分布(
はガンマ分布(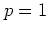 ,指数
,指数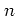 )に従い,期待値
)に従い,期待値
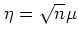 である.仮説は
である.仮説は
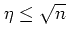 とする.
とする.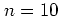 ,
,
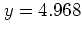 とすれば,
とすれば,
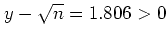 であり
であり
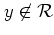 となる.実はちょ
うど
となる.実はちょ
うど
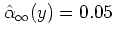 となるように値を選んである.
となるように値を選んである.
数値例1と同様に計算を行うと,
から
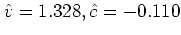 が推定される.確率値は
が推定される.確率値は
である.
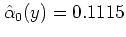 に比べれば
に比べれば
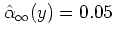 に
近いものの,必ずしも精度が高くないことが分かる.
に
近いものの,必ずしも精度が高くないことが分かる.
前節では正規モデルを仮定していたが,一般の指数型分布族では
と書ける.ただし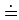 は両辺の誤差が
は両辺の誤差が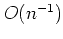 で
あることを表す.
で
あることを表す.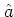 は加速定数と呼ばれ,確率モデルの性質と
は加速定数と呼ばれ,確率モデルの性質と
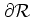 から定まる量である.正規モデルでは
から定まる量である.正規モデルでは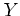 の分散行列が単位行列に
固定されていたことが本質的であり
の分散行列が単位行列に
固定されていたことが本質的であり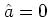 であった.一般の指数型分布族で
は,
であった.一般の指数型分布族で
は,
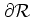 の法ベクトル方向に関して,
の法ベクトル方向に関して,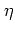 を動かしたときの分散の
変化率が
を動かしたときの分散の
変化率が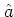 に反映されている.
に反映されている.
Efron (1987)のABC法によれば,3個の幾何学的な量
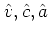 を用いて
不偏な確率値は
を用いて
不偏な確率値は
と表現される.一方,前節の方法で計算した確率値は
であり,
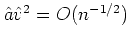 だけ誤差が
ある.これを補正するために,
だけ誤差が
ある.これを補正するために,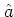 を推定する必要がある.
を推定する必要がある.
平成16年7月12日
![]() が期待値
が期待値![]() の指数分布に従うとき,
の指数分布に従うとき,
![]() はガンマ分布(
はガンマ分布(![]() ,指数
,指数![]() )に従い,期待値
)に従い,期待値
![]() である.仮説は
である.仮説は
![]() とする.
とする.![]() ,
,
![]() とすれば,
とすれば,
![]() であり
であり
![]() となる.実はちょ
うど
となる.実はちょ
うど
![]() となるように値を選んである.
となるように値を選んである.
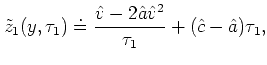
![]() を用いて
不偏な確率値は
を用いて
不偏な確率値は