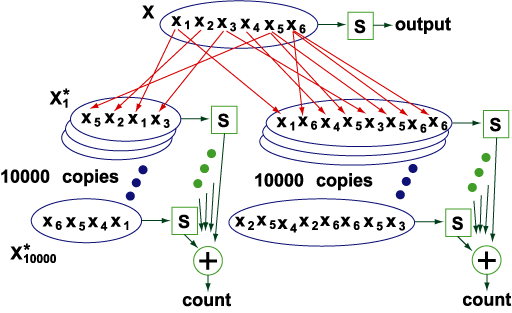
多重リサンプリング法(マルチスケールブートストラップ法)の概念図
2002年5月
下平英寿
確率モデルに基づいてデータから有用な情報を引き出す数学的方法は科学や産業の様々な分野で用いられている.実際の応用ではモデルの構造やパラメタ値が事前に確定せず,それらは多くの場合データから推定される.これをモデル選択と呼び赤池情報量規準をはじめとする様々な方法が開発されている.以下ではモデルを一般に「仮説」を意味するものとして広くとらえる.データには何らかの意味でバラツキがあるから,データから計算して得られるモデル選択の結果もバラツキがあるはずである.従って手元のデータから選択したモデルは必ずしも妥当とは言えず,より多くのデータを用いた再分析によって以前の結論がしばしばくつがえされる.例えば哺乳類のDNAシーケンスを分析しその違いから図2左のような進化の順序(系統樹)が推定され数年前のNature誌に報告された.従来ウサギとマウスは近縁であると考えられていたので,ウサギはむしろヒトに近いという仮説を意味する図2左は驚くべき結果であった.ところがその後得られた最新データも加えて再分析すると図2右が支持されて結局ウサギとマウスが近縁だとする従来の仮説に戻ってしまった.もちろん図2左を得る際にはデータのバラツキを考慮して結論が統計的に有意であると仮説検定によって示されていた.それでも一定の確率で誤った結論に至るはずだが,問題なのはその誤り確率が必要以上に高いことである.場合によっては互いに矛盾するいくつもの仮説が報告されており,それぞれの主張の正しさが統計的に有意な証拠で示される.
この問題の本質は仮説の多重性にある.多くの仮説を同時に調べると仮説の一つが「まぐれ」で有意に見える可能性が高くなる.この選択バイアスと呼ばれる効果を正しく補正しないとfalse positive によって誤り確率が増えるのである.先ほどの6種の哺乳類の可能な系統樹の形は105通りあり,これらが同時に調べられていたことになる.種の数を増やすと可能性は組み合わせ的に増大する.近年様々な分野で多量のデータが蓄積されるに伴い,データマイニング等と称して非常に多くの仮説が同時に探索されるようになってきている.このような状況でも仮説の妥当性を定量的に正しく評価できる方法の開発は非常に重要である.
多くの候補となるモデル(すなわち仮説)についてその妥当性をデータに照らし合わせて定量的に評価し,それぞれのモデルについて確率値として表現する方法が本研究のテーマである.非妥当性が有意に示されないモデルを選び出してきてこれを列挙したものがモデル信頼集合であり,データから予想されるシナリオの一覧と解釈できる.先の例では図2左の他に図2右を含む複数の系統樹が列挙される.本研究では特に多重リサンプリングというアイデアを基礎に,(i) 新たな方法論の開発と数理統計的な解析, (ii) ソフトウエアの開発と配布, (iii) 現実の問題への応用の3段階の研究を行う.
データからモデルをひとつ選択する方法(ソフトウエア; 先の例ではクラスタリング法)が諸分野で開発されている.これをサブルーチン的に多数回呼び出すだけでその中身を知らなくても容易に仮説の多重性を補正したモデルの確率値とモデル信頼集合が高精度で計算できるという「プラグイン」原理が本研究の大きな特徴である.これは一種のモンテカルロ法であり計算量が莫大になるものの,データ解析の広範な問題に直ちに適用できる.リサンプリングの標準手法であるEfron (1979) のブートストラップ法はFelsenstein (1985)によって確率値の計算に用いられたが1次の漸近精度のため選択バイアスは補正されない.Efron ら(1996) の方法は2次の精度である.本研究のアイデアでは原理的に3次の精度が達成され選択バイアスが自動的に補正されるだけでなく実装が容易であることが応用上重要である.選択バイアスは多重比較法によっても補正されるが本研究の方法に比べて結果が保守的である.ダブルブートストラップは本研究と同様の性能を持つが,本研究に対して2乗の計算量が必要になり非現実的である.これまで多重比較法による解析を行い実績のある進化系統樹推定をはじめとして,マイクロアレイやSNP 解析などのバイオインフォマティクスの諸問題,さらに計量文献学への応用を具体的に準備している.ソフトウエアの一般公開によりこの他の分野(例えば金融工学) でも応用が期待される.
先行研究として下平(1993), Shimodaira (1998) の多重比較法をモデル選択に適用するというアイデアはそれまでにない独創的なものであった.これを進化系統樹解析に用いた Shimodairaand Hasegawa (1999) の方法は自ら公開したソフトウエアに加えて Shimodaira-Hasegawa test として PAUP*, Phylip, PAML, PAL 等の代表的な系統樹解析ソフトウエアにオプションとして最近実装された.さらにCambridge 大学のGoldman ら(2000, Systematic Biology) のレビュー論文で報告されるなどして,この分野の標準手法となりつつある.Shimodaira and Hasegawa (1999)の被引用回数も最初の2年間で36となりその後も順調に増えている.これらの応用を通して多重比較法の保守的な性質が大規模問題で障害になることを実感し,より性能の良い手法の開発を試みるに至った.このためのひとつのアイデアが最近得られた多重リサンプリング法である.これまでにある種の限定された状況においてその3次の精度が数学的に証明され,また最近公開したソフトウエアにその方法を一部実装した.より一般的な状況では2次の精度まで理論的には実現しており,さらに新しいアイデアを探索中である.このように新しい方法論を開発し,それをソフトウエアに実装するための準備は十分にできている.また進化系統樹の分野における応用研究に関しては十分な実績があるので比較的容易に可能である.この他のバイオインフォマティクス等の応用研究に関しては共同研究の相手との準備をすすめている.
Efron (1979) のブートストラップ法は一種のモンテカルロ計算であり,データ自身からそのバラツキを反映したコピーを多数生成するリサンプリングの標準手法である.各コピーがどのモデルを支持するかを数え,その頻度が高いモデルほど妥当性が高いと考える.通常はコピーにおけるデータサイズはオリジナルデータと等しいが,多重リサンプリングではデータサイズを変えながら複数のブートストラップセットを生成する.これは問題のスケール(オーダパラメタ)を変えることに相当し,これと支持頻度の変化率から確率値の計算に必要な情報が得られる; (Shimodaira 2000, Stanford Univ. Stat-TR35). つまりFisher 情報行列を計量とする双対幾何 (Efron-Amari 情報幾何理論) におけるモデルの多様体の曲率と計量の変化率および符号付尤度が多重リサンプリングから計算される.古典的な数理統計の多くの解析的な結果が計算機による数値シミュレーションで近年置き換えられている一方でこのような新しい状況における理論が必要になっている.

多重リサンプリング法(マルチスケールブートストラップ法)の概念図